Tullock, Application of Economics in Biology

Source: An essay in Toward Liberty: Essays in Honor of Ludwig von Mises on the Occasion of his 90th Birthday, September 29, 1971, vol. 2, ed. F.A. Hayek, Henry Hazlitt, Leonrad R. Read, Gustavo Velasco, and F.A. Harper (Menlo Park: Institute for Humane Studies, 1971).

An Application of Economics in Biology by Gordon Tullock

(It may seem odd to place an article originally designed for publication in a biological journal in a collection of articles dedicated to Ludwig von Mises. Among his other distinctions, however, Professor von Mises was among the first to point out that economics can be expanded to deal with many areas outside of its traditional scope. In my own case, my work in expanding economics into new areas was, in a real sense, begun by my reading of Human Action. The article below, then, represents my most extreme application of economics outside its pre-von Mises boundaries.)

The recent rise of interest in problems of pollution and similar matters has led to considerable contact between those biologists interested in ecology and economists interested in the special economic field of “externalities.”1 It is the point of this essay to indicate that there are certain interrelations between the economics of externality and the problems of ecology, which are different from those ordinarily studied. Specifically, I propose to use the economics of externality as an analytical tool in dealing with natural ecological systems. Plants and animals have effects on other plants and animals, and the effects of these externalities are very much the same as the externalities which human beings impose on each other or upon the natural environment.

The results of this investigation will be, I think, somewhat startling to the biologist. I think I can demonstrate that the climax state of any ecological system is inferior. That, substantially, regardless of what value we put upon the individual species within the ecological system and/or their usefulness to man, it is nevertheless possible always to improve upon the system produced by “nature.” In order to make such a judgment which will fit any one of a vast number of different sets of values, I will be compelled to make use of an economic concept, known as Pareto optimality, albeit in a radically reformed manner. Pareto optimality was first suggested as a way of avoiding making certain types of value judgments, and it can be used in evaluating biological systems in a similar way.

For the purpose of this article, I propose to use a very simple system. This simple system will not exist anywhere in the real world—it is too simple for that—but it closely approximates a situation which we do find very commonly in the real world.2 The system is composed of two species: grass and some herbivore. One may consider it to be an approximation of the situation in the Old West in which cattle grazed upon grasslands.3 For the time being, we will assume that these are the only two species. This simplification is introduced in order to make the line of reasoning easier; it can be demonstrated that the same principles apply even if we have many species and the ecology is quite a complex one. This demonstration, however, will not be included in this article, since it is quite complicated and the outcome seems intuitively obvious.

Under these circumstances, we may feel fairly confident that what is known as “over-grazing” would occur. The cattle would multiply until such time as there were enough cattle exactly to consume the maximum amount of grass produced by the plot. This grass, however, in part would be produced by mature plants; in other words, it would be possible for the number of cattle temporarily to rise to a larger number than could be permanently maintained by the process of eating the existing plants back down to the point where they no longer are fully efficient. In a sense, this is consumption of capital in the form of grass to support additional cattle.

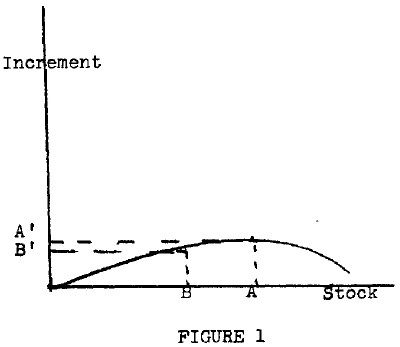
In order to make the matter clear, let us turn to Figure 1. On the horizontal axis, I have shown varying amounts of grass that could be on our plot of land. The vertical axis then shows the increment that one could expect in a short period of time, let us say one day, granted that you have that amount of grass shown on the horizontal axis at the beginning of the time period. If you have very little grass already in existence and, hence, are on the left end of the horizontal axis, there will be relatively little growth in any given short period. Similarly, if the grass is already up to the maximum that the land can hold, there will be no increment; hence the line once again hits the horizontal axis.

Between these two points, the increment rises as the amount of grass increases, and eventually falls off. If we propose to harvest the maximum amount of grass that we can from this plot, we should choose to maintain the stock of grass at amount A and harvest, during this period, A' of grass. Assume that our method of harvesting the grass is to let cattle graze upon it. You should also assume that the line drawn represents the amount of grass which the cattle can take in each day, although in practice this line would probably be somewhat below the physical increment in our diagram, because the cattle are not perfectly efficient in removing grass in such a way as to inflict the least possible damage on the remaining grass.

Suppose, then, that we attempt to graze more cattle on the land than can be supported by eating the grass A'. Under these circumstances, they would eat not only the increment in any given period, but some additional grass, let us say the amount A-B on the horizontal axis. As a result, in the next period the total amount of grass available to produce more grass would be smaller, hence only B' amount of grass would be produced. Under these circumstances, the cattle would once again cut into the existing stock and move us farther to the left. Eventually, we would reach a situation in which grass was scarce, and the few scrawny cattle which grazed upon it would find the energy involved in chasing down their grass enough so that they could not increase in population. Under these circumstances, a new equilibrium would be reached somewhere to the left of A.

Hereditary selection of the “fit” makes this outcome inevitable. If some of the cattle had a relatively low rate of reproduction and others a rather high rate of reproduction, and the cattle with the low rate of reproduction had a rate of reproduction such that they remain in exact balance with the grass supply, the only effect of this would be that in each generation there would be more cattle of the high reproduction strain and a lower percentage of cattle in the low production types. The death rate from overgrazing would be spread across both types, independently of these reproductive capacities; hence the end product would be the gradual disappearance of the low reproduction strain.

Note the situation, however. By artificially restricting the number of cattle, we can increase the amount of grass produced each year and, thus, in the long run produce more cattle. It is possible by intelligent management to produce a situation in which both more grass and more cattle (or both elements of our simple ecology) exist than would exist under natural climax conditions. Suppose that point B in Figure 1 is the natural climax with the amount of cattle which consume exactly B' grass. Under these circumstances, by reducing the number of cattle temporarily, one could increase the amount of grass and make it possible to maintain a larger number of cattle on the same land in the future.

Intelligent range managers do exactly this. A well-functioning cattle ranch supports more poundage of beef animals than it could support if the manager did not artificially keep the grass and the beef in balance. This balance is essentially an artificial structure which could not occur in a state of nature, and the natural balance would involve less of both grass and cattle. The movement from the cattleman's organized ecology to natural balance would involve a natural (and temporary) increase in the number of cattle, which would then graze back the grass supply. Similarly, a movement from the natural ecological balance to the cattleman's superior ecology would involve a temporary restriction of the number of cattle in order to permit the grass to grow up to a higher level of productive efficiency.

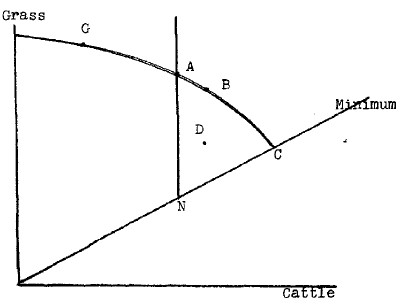
Ranch managers, in dealing with this kind of problem, have a fairly simple and straightforward objective: they want to maximize the production of beef or whatever else it is they are raising. Our system, however, has no such obvious maximum. Consider Figure 2. On the vertical axis, I have put the total amount of grass on some particular plot of land, and on the horizontal axis, the total number of cattle. Since there is some minimum amount of grass necessary to sustain each head of cattle, I have drawn in a line representing this minimum, starting at the origin. In actual fact, the line would probably be slightly concave downward and not quite hit the origin, due to the fact that the cattle must use more energy to seek out grass when it is scarce, but we can ignore this minor correction. All of the points in the area above the minimum line and below the curving line GABC, are feasible, i.e., it is possible to reach any combination of grass and cattle shown in this area.

The line, GABC, is the maximum amount of our two species which can be supported by the land in varying combinations. It corresponds to the production frontier of standard economic theory. The maximum amount of cattle which can be raised or the cattleman's maximum is shown at C. Similarly, the maximum amount of grass which can be raised is shown at G. Note that G is not drawn at the vertical axis, because I assume that the fertilizer produced by the cattle has at least some effect in stimulating grass production. This might not be so in some circumstances, in which event the maximum grass production would be obtained without any cattle at all. The other points on the line GABC represent other combinations of production of cattle and grass, and in each case they are maxima, i.e., you cannot produce more with the same ratio. The area within the production frontier and above the minimum, which after all is simply part of the production frontier, represents those combinations of cattle and grass which are achievable, but are less productive than the areas on the frontier.

Let us suppose that N is the natural climax or equilibrium of the system. It is the point to which the system will proceed if there is not regulation on the number of cattle. Any point in the triangle—bounded on the bottom by the minimum line, on the left by the vertical line drawn through N, and on the upper right by the curved line ABC—is superior to N in production of grass and cattle. Any point in this area will be better from the standpoint of both increasing grass production and increasing cattle production than is N.4

Note, however, that there is a good portion of the production frontier—that running between the vertical axis and the vertical line running through A—which we cannot say is clearly dominant over the natural climax. In order to make any judgment here, we would have to have some way of evaluating grass against cattle. If we did feel that grass was much more important than cattle, we would probably aim at point G, even though this would reduce the number of cattle. But this requires a value judgment; movement up and to the right from N requires no judgment as to the relative merits of grass or cattle, it merely requires a feeling it is desirable to have more. Hence, if movement into this triangle is movement into a permanently sustainable system, it seems hard to argue against the view that we would have as much of the natural product as possible. Certainly, the ecology buffs cannot complain about it.

It is very hard, however, to decide what specific movement from N would be optimal without some kind of value system putting cattle against grass. Movement out to point D and then on, let us say, to point B clearly involves two improvements from the standpoint of both cattle and grass. From the standpoint of the grass, however, A would be better and from the standpoint of the cattle, C would be better. Here we are confronted with a situation which frequently confronts economists, and we shall follow the economist in refusing to solve the problem. With an external value system, we could decide which point was the best. Without such an external value system, however, all we can say is that our diagram shows a number of points which are superior to the natural equilibrium point, but gives us no way of choosing among these points. Since any one of them is superior to the natural equilibrium, on the whole movement to any one of them would be desirable. The decision as to which point on the frontier is optimal is equivalent to the distribution problem in economics, and, as in economics, can only be solved by bringing in external value judgments. I have no objection to the reader bringing in such a value judgment, but I suspect that the readers have different judgments. We can all agree, however, that movement up and to the right would be desirable, even though we might disagree as to which of the various directions within the pieshaped space would be optimal.

So much for our simple two-species ecology. Let us now engage in a somewhat more rigorous investigation of the tools which have been used in this example, and then indicate how a more general version of these tools can be applied to a more realistic ecology. First, note that we have had only two species on Figure 1. Economists have discovered that a simple two-item diagram like this can be a great help in analyzing many-dimensional situations. The real ecology could be placed in a multidimensional space with each species, or indeed each subspecies, on a separate dimension. This hyperdimensional diagram would then have a hypersurface, its equivalent of the curved line, and there would again be an area inside this which was achievable but not fully efficient.

A simple two-dimensional diagram which can, after all, be drawn on a piece of paper can be thought of as a cross-section of that much more complex diagram. Alternatively, it can be considered to be a special two-dimensional space in which one of the axes is a particular species and the other is a composite bundle of all of the other species. By this method, each species can be taken out by and of itself and its interrelation with the whole ecology (minus itself) analyzed. This latter technique is perhaps less convenient for ecological problems than it is in economics, because in economics we have a rather simple measure of the purchasing power. We can consider the baskets of goods which are being contrasted to the single good as having whatever their monetary value is.

The most elegant way of dealing with a manydimensional space with many species, each represented by one dimension, would of course make use of the Cartesian algebra in its many-dimensional version. Although this is the most elegant method, it is generally speaking much too tedious and, in any event, we seldom have enough empirical knowledge to make it sensible to move to such a complicated representation. Nevertheless, it should always be kept in mind that this many-dimensional Cartesian system is the true model, and the twodimensional subset of that model is a simplification.

A second special problem has to do with values. It is good Catholic doctrine that the natural world exists solely for the benefit of man, and that man, therefore, is the measure of the ecology. This would, needless to say, raise the question of which man; hence, we would be back to the distribution problem of economics. There is, however, an even more fundamental difficulty here. A great many people are now saying that they do not think that man should be the measure of all ecological problems, and that we should take into account the well-being of other species. In part, these people are simply expressing themselves badly. Many of them do in fact hold the well-being of mankind as their major goal, but feel that long term calculations of the well-being of mankind require some temporary sacrifices of human well-being in the aid of the well-being of certain other species.

In this sense, there is no particular problem with our diagrams. The point on the efficiency frontier would be the long-run sustainable output; hence we could still retain the desire to maximize the return for human beings. In Figure 1, since human beings do not eat grass and do eat cattle, we would choose point C. Some of the members of the Sierra Club, however, apparently do believe that it is worth sacrificing some long-run human goals for long-run growth of other species. For them, the value system is not quite so straightforward.

Fortunately, the Paretian apparatus makes it possible for us to deal with this matter without much difficulty.5 The Paretian apparatus was first designed for the specific purpose of dealing with some change which might injure one person and benefit another. It was pointed out by Pareto that we had no positive reason for believing that the injury and the benefit were commensurable. It might well be that what we thought was a rather minor injury to Mr. A actually hurt him more than the benefit received by what to us appeared to be a very significant improvement for Mr. B. Pareto, therefore, suggested that we accept a very modest criterion: any change which benefits at least one person and injures no one must be an improvement. It is clear that this rule gives guidance only in a general way. Returning to Figure 2, it indicates that we should move up and to the right from point N, but does not tell us the exact location. It is an astonishing fact that this very simple rule has permitted a very large amount of calculation on improvement in the economic system. I hope to demonstrate that it will be of almost equal use in the biological system.

For people who have strong personal feelings on the evaluation of different species, the rule will not be ideal. They might feel very strongly that some particular point on the frontier shown in Figure 1 is superior to all others. There is no reason why they should not feel this way and they can, of course, make calculations very similar to the ones I have made; thus, they get results which are in essence a specialization of the very general results I get. The advantage of the very general results, however, is that they are not dependent upon the particular value system of the investigator. We do not have to choose between grass and cattle to accept a movement up and to the right from point N. If I am interested in the well-being of either human beings or of these particular species or any one of them, such a move is an improvement, even though it may not be a movement toward the point which exactly maximizes my particular goal. If, for example, I was pro-grass, I would regard movement from N to D to be an improvement; but I would regard any point between A and C as inferior to G. Such a move, however, would be a marked improvement over N.

The system, thus, is relatively value-neutral simply because it is consistent with a tremendous range of possible values, not because it imposes any value system of its own. Individuals are likely to regard their own personal value system as better than this criteria which, instead of aiming wholeheartedly at fulfilling their value, aims at giving at least some benefit under a very large range of values. The principal argument for the Paretian rule is that it does avoid most of the controversies which any more specific rule would entail. Actual decision in any specific case must involve putting in more in the way of a preference function than the Paretian rule. The Paretian rule demonstrates in Figure 1 that improvements are in fact possible; it does not specify which of the many improvements should be undertaken.

Let us now discuss the concept of externality. Externalities were originally developed in economics to analyze certain areas where the market economy worked badly. They are probably more familiar to biologists than most other tools of economics simply because the problems of pollution are very good examples of externalities in the pure economic sense. We, however, are not talking about externalities generated by human beings, but externalities generated by plants and animals.

Externalities are rather easily understood. Any given species will have some effects upon the development of some other species. The grass, for example, provided a food for the herbivores and the cattle reduced the total amount of grass by eating it. In the first case, we have a positive externality, that is, a species providing something of benefit to other species; and in the second case, we have a negative externality, that is, a species doing something to injure another species.

We need not, however, confine ourselves to these very direct relationships of eating and being eaten. Most plants release into the soil and into the atmosphere various chemicals. The obvious case, of course, is free oxygen into the atmosphere, but there are many others. Confining ourselves to chemicals found in the soil, we find that these chemicals have an effect upon the soil which makes it more or less suitable for the growth of other plants. This is an example of an externality. There are innumerable other similar examples. Indeed, in a real sense, the whole science of ecology is devoted solely to the study of such externalities. The existence of one plant or animal has significant effects on many other parts of the ecological community, and the study of this chain of effects from each plant or animal to all the other plants and animals is the subject matter of ecology. I will not, however, make an effort to develop the collection of interactions in any existing ecology, but to discuss the theoretical consequences of the mere existence of such interaction.

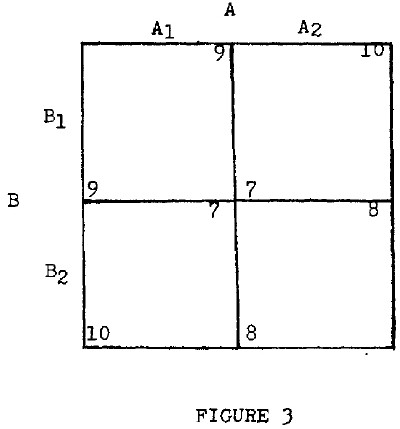
Let us begin our discussion with a very simple example. We assume two plants which customarily live in close proximity and we assume that each produces, as a byproduct to its life processes, a chemical which is of benefit to the other. Thus, each plant will grow somewhat better in the presence of the other.6 Here we have an externality. Naturally the plants, having no minds, do not take this externality into account; but evolution will select the plants for efficiency in generation of these byproducts as well as for efficiency in other matters. We can, therefore, discuss what is the most efficient rate of generation of the byproduct for the plants and, as we shall see, the rate of generation of the byproduct which would be selected by natural selection is inferior to another rate. The details of this argument are quite complex, but we may begin by simply assuming that each of the plants is available in two strains, as shown on Figure 3. Species A is available in variant A1 and A2. A2 produces the byproduct only insofar as that byproduct is essential for the maximization of the growth of the strain in and of itself. In other words, it spends no energy at all on producing additional amounts of that byproduct. A1, on the other hand, sacrifices some of its own growth in order to produce more of the byproduct. With species B, the same situation obtains, with B2 being the strain which produces only enough of the byproduct as is consistent with maximum growth of itself, and B1 being the one which produces more of the byproduct and which tends to get somewhat less growth itself.

In the figure, the weight of each of these plants which, given a space of land (granted there is a mixture of the two), can be expected to support is shown with A in the upper right hand corner and B in the lower left of each cell. Since each species byproduct benefits the other species and since, in this case, the benefit is “Pareto relevant,”7 the weight of each plant is higher in the upper left hand corner where each of the plants is using some of its energy to provide “fertilizer” for the other than in the lower right, where each of the plants is composed of the “2” strain, which simply attempts to maximize its own development while ignoring the development of the other. Both types of plant have a higher net weight in this upper left square than in the lower right; hence, the upper left can be regarded as being superior from the standpoint of either plant.

Note, however, that the structure of this diagram is that of the prisoner's dilemma. It is clear that the strains which would be selected by natural selection are not A1 and B1, but A2 and B2. We can see this very easily by observing that if a mixture of A1 and A2 were placed in a field with either B1 or B2 (or a mixture of them), the A2 would grow more rapidly than A1, as shown by the matrix. Over a number of generations, A2 would completely replace A1. For example, if the strain of B which happened to be in the field was B1, then a given amount of plant seed for A2 would produce ten-ninths as much as the same amount of plant seed would for A1. Similarly, if the field was planted in B2, the ratio would be eight-sevenths. Since the diagram is symmetric, the same line of reasoning applies to B. Thus, natural selection would select strains which produce a lower quantity of these plants than other strains. With selective breeding, it would be possible to produce strains which produced more of both of the two plants.

Needless to say, positive externalities of the sort shown in Figure 3 are not the only ones we find in nature. Plants may also cause great injury to or exterminate other plants, and the same is, of course, true of animals. We could make up an example similar to Figure 3 to deal with such cases, and we would find once again that the natural selection optima would not be that which maximizes the output of the two strains. Further, the use of two strains is dictated only by a desire for simplicity. We could have a very large number of strains and, for that matter, mixtures of different strains. The end product would be the same. Further, the use of two species instead of the many-species of the average ecology is dictated solely by the fact that I am using a two-dimensional piece of paper. The argument is, in fact, much stronger if there are many species than if there are only two. Thus, nature unaided does not reach an optimum.

REFERENCES

[1]Otherwise referred to as neighborhood effects or public goods and bads. At this point, I shall not include a technical definition of externalities since the meaning of the term will become clear to the reader as he goes along. I should perhaps warn economists that the word, although within the normal scope, will have somewhat different applications than the one to which he is accustomed. For some recent literature showing the contact between biologists and economists, see Hardin (1968) and Tullock (1970, 1971).

[2]This situation has been considered a great deal by economists, particularly those concerned with the undeveloped areas, because of its relationship to meat production by pastoral activities. Economists, of course, have considered it solely in terms of its long run effect on the human beings who engage in pastoral activities in the areas concerned. We will be considering it without this ethnocentric bias.

[3]Although I have chosen to illustrate this example with cattle and grass, the same system exists in many natural situations. One example is presented by J. P. Dempster (1968).

[4]This is, of course, the standard Pareto criteria and it should be noted that movement along the vertical line through N would increase grass production, but not cattle production. Thus, we would be increasing one and holding the other constant. This is what leads to the Paretian slogan: improve the welfare of one unit while injuring no one. In practice, of course, we seldom are able to move along the boundaries and, therefore, benefit both or all of the factors.

[5]Note that in strict terms, there is no way in which we can avoid maximizing the utility functions of human beings. The members of the Sierra Club are human beings; if they feel that it is better to have a smaller population of human beings and a larger population of redwoods, they are maximizing their own utility functions when they aim at or achieve this goal. Redwoods cannot vote. Thus, in a sense, any policy carried out by human beings will aim at the maximization of at least one human being's utility function, rather than at some other goal. The well-being of nonhuman species comes in only insofar as some or all human beings may have the well-being of such nonhuman species as arguments in their utility function.

[6]In many cases, the chemical persists in the soil so that the history of the area may be more important than its current use. This would, however, merely strengthen the relationships discussed.

[7]The concept of “Pareto relevance” is rather complex, but in this case it can be interpreted very simply. As long as the numbers in the upper left hand corner are larger than those in the lower right, the externality will be Pareto relevant. This is not, of course, a necessary condition in the real world. We would anticipate that sometimes we would find it and sometimes we would not.